PhD Thesis Final Defense to be held on October 30, 2019, at 14:00
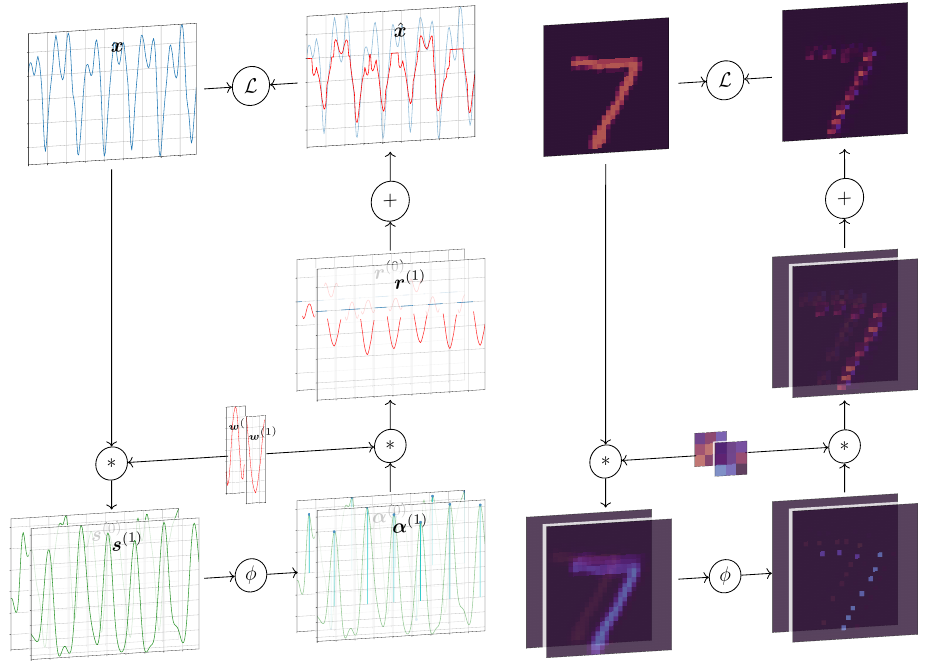
Photo Credit: Paschalis Bizopoulos
The examination is open to anyone who wishes to attend (Teleteaching Room 1, Central Library of NTUA).
Thesis Title: Sparsely Activated Networks: A new method for decomposing and compressing data
Abstract: Recent literature on unsupervised learning focused on designing structural priors and optimization functions with the aim of learning meaningful features, but without considering the description length of the representations.
The result of this PhD thesis is the introduction of a novel Neural Network architecture, Sparsely Activated Networks (SANs), which decompose their input as a sum of sparsely reoccurring patterns of varying amplitude, and combined with a newly proposed phi metric they learn representations with minimal description lengths.
SANs consist of kernels with shared weights that during encoding are convolved with the input and then passed through a sparse activation function.
During decoding, the same weights are convolved with the sparse activation map and the partial reconstructions from each weight are summed to reconstruct the input.
We also propose a model selection metric phi, that favors models which combine high compression ratio and low reconstruction error and we justify its definition by exploring the hyperparameter space of SANs.
We compare five sparse activation functions (Identity, ReLU, Max-Activations, Max-Pool indices, Peaks) on a variety of datasets and show that SANs learn interpretable kernels that combined with the phi metric, they minimize the description length of the representations.
Keywords: neural networks, autoencoders, sparsity, compression
Supervisor: Koutsouris Dimitrios, Professor
PhD student: Paschalis Bizopoulos
