The use of Convergence Acceleration Methods (CAMs) in antenna-engineering applications
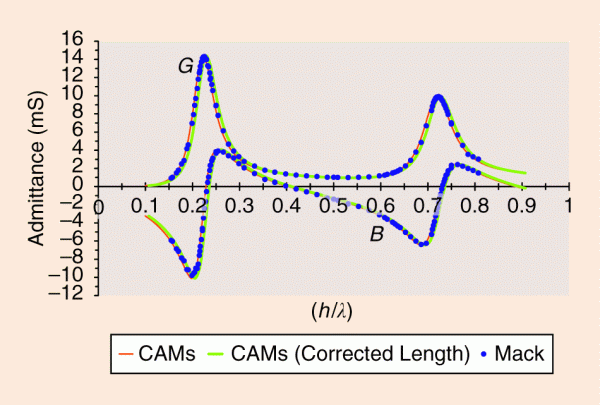
Figure: The computed and measured admittances for 0.1≤h/λ≤0.9, a/λ=0.007022, and b/a=3 . The abscissa is h/λ and the points (dots) correspond to the real and imaginary parts of YMack(h/λ) . The solid curves illustrate the real and imaginary parts of YTh(h/λ) (thin line) and YTh((h−a)/λ) (thick line).
Solving thin-wire integral equations is one of the most-discussed problems in the theory of antennas.
A paper by A. Marinakis, P. J. Papakanellos, and G. Fikioris, recently published in IEEE Antennas and Propagation Magazine ( Vol.: 62, Issue 3, June 2020), shows that properly selected Convergence Acceleration Methods (CAMs) can be utilized for obtaining rapidly convergent answers from sequences of results obtained from popular and simple numerical methods applied to antenna integral equations.
Specifically, CAMs are applied to predict driving-point admittances of thin-wire dipole antennas. It is shown that the selected CAMs are indeed capable of providing substantial convergence acceleration. Some “good” electromagnetics engineering practices, such as the use of the so-called "exact kernel" in the dipole integral equation and the "magnetic-frill generator," are applied to obtain reliable theoretical values of driving point admittance. The result is a much better agreement to the very well-known experimental results of R. B. Mack, obtained when Mack was a student of R. W. P. King at Harvard University.
Read more at DOI:10.1109/MAP.2020.2983982
